講師コラム：足立　堅一　先生

統計解析に詳しい足立堅一先生のコラムをお届けしております。
コラムへのご意見、ご感想がありましたら、こちらまでお願いします。

『 どこにも書いてない、誰も教えてくれない「統計解析」
－本当に重要な“勘どころ”とは－ 』

問題２－１　自分が関連する分野・場合において、因果推論的観点が有効であるかどうか考察すること。その理由は何か？

　次回は、現代統計学の枢要な概念である「母集団と標本」とそれに関してほとんどの者がしでかす誤解について述べる。
　
１）　日本化薬（株）診断薬室 「目からウロコの医学統計学講座」

　
[topへ]

---

第3回　生物統計学の枢要な概念とその特長と流布する誤解　（2007/08/07）
　
　以降の解説は、現代統計学、つまり推測統計学、その中でも取り分け、「生物統計学」に焦点を絞ることにする。今回は、「母集団　vs. 標本」という重要な概念が、しばしば理解されず、そのことに起因する誤解を指摘して、それらからの脱却への道を示そう。
　
３．１．枢要な概念としての「母集団　vs. 標本」　
―　象徴的な例を挙げられるか？
―　「近頃の若い者は」に秘められた「母集団　vs. 標本」という重要な概念の萌芽
　世のオジサン(オヤジサン)の言としての「近頃の若い者は．．．」は、余り歓迎されないようであるが、実は、そこには、「母集団　vs. 標本」概念の萌芽がある素晴しいものである。その理由を、解説しよう。それは、こうである。
(1)オジサンが観測可能な若者は、当然ながら、先ずどう頑張っても、有限の若者達になってしまう。(また、おそらく身近の若者達だけとなる。)
―　実は、これが「標本(sample)」なのである。そして、日常用語である「data」がしばしばこれに相当する。
(2)しかし、オジサンが下す、「近頃の若い者は」との結論は、彼が観測した若者達に限定されるものでは決してない。それは、明らかに、未だ見ぬ若者達を包含するものであり、彼らへも敷衍/一般化されるものである。噛んで含めた解説をすると、「近頃の若い者は挨拶もできない」との結論は、オジサンが観測した若者達だけがそうであり、未観測の若者達がそうであるかは関知しないとの意味では決してない。従って、そこには、或る意味での飛躍があり、これがまた現代統計学誕生のための飛躍とも言える価値あるものとも言えよう。
　これは、本邦に限定しても、対象・標的は、北は北海道から南は沖縄までの若者である。これはまさに、「国勢調査」の類に該当する。
―　実は、この「敷衍/一般化される対象」が母集団(population)」である。
　
３．２．「標本」に限定した「結論」 vs. 「母集団」へと波及する/させるべく「結論」
―　　ほとんど全ての場合が、「母集団」へと波及する/させるべく「結論」
　ここで、注目すべきは、オジサン一人では、これだけの多数の若者を面接することは、事上不可能ということである。また、オジサンのcaseでは、結論を観測した若者達に限定することにして、必ずしも一般化することは必要ないのかも知れない。しかし、現実に生物統計学が適用される場においては、ほとんどの場合に一般化が必要なのである。例えば、１０人の患者に薬剤を投与して、８人に有効であった場合の結論「この薬剤は８0％の有効率である/あった」との意味を深く洞察してみよう。
その意味は、「この薬剤は、当該１０人には８０％の有効率であった」というだけの結論であり、次の別の１０人でどうこう言うつもりは毛頭なく、全く無効だって構わんし、そんなことは知ったことではないということであろうか？　そうではない’　その結論を当該１０人だけに限定することを目的としている訳では決してない。その逆で、この１０人で８０％有効であったので、他の未投与の患者さんに対しても、その程度の有効率が期待できるというのが結論としての標的なのである。ここで、問題を意識化/顕在化するために問題の形として提起しておこう。
　
問題３－１　自分が統計学を使っている分野・場合において、結論の出し方としては、手中のdataに限定した結論で十分であるものか、それとも「近頃の若い者は．．．」流の結論であるべきかを具体的例において考察すること
問題３－２　時間と金を厭わないとして、全ての患者への薬剤の効果を観測することは、可能か？
―　不可能であることを考察すること
　
３．３．「結論」を「母集団」へと波及するときの注意点
―　精度(precision)という概念の導入
　「２打席１安打」の打者が「俺は５割打者」だと言ったら、信じる/られるであろうか？　１０打席５安打ではどうであろうか？　２０打席１０安打、５０打席２５安打、１００打席５０安打では？　５００打席２５０安打では？　直観的に、この順番に信頼度・確信度は上昇する。 この直観は、現代統計学用語では、象徴的には「信頼区間(confidence interval)」で表現される。
　つまり、例数の増大とともに、確信度は上昇し、これは換言すれば、誤差の減少・精度の向上ということになり、信頼区間幅の減少に帰結する。先ほどの有効率の例では、１０例での８０％有効率と１００例での８０％とでは、後者よりも前者は誤差が大きく、精度は悪いということになる。ついでに、言ってしまえば、例数無限大のときに、誤差０、精度１００％(不確定の指標と言える信頼区間→0)となる。
　
３．４．現代統計学の特長とは何か？
―　目的に応じて、精度を必要最低限の程度に制御することで、少数例(標本)で得られた結論を母集団へと一般化すること
―　cost-performanceの追求
以上のような概念を導入することにより、現代統計学が追及し獲得したものは、可及的に少ない標本で得た結論を母集団へと一般化する法ということになろう　^{1) 2)}。
　以上のことを表３－１にまとめておこう。
　
３．５．現代統計学の消化不良に起因する流布する誤解
―　あなたも犯している？基本的かつ恐るべき誤解！
　おそるべき社会現象として、しばしば、１０人中８人までもが、平気な顔をして「今回の試験では、母集団/母数が少なくて確かなことが言えない」などという表現をするのを聞いて驚愕する。「今回の試験では、例数/標本が少なくて確かなことが言えない」というべきである。問わず語りに現代統計学の基盤となる概念に関して、自らの無知・無理解を暴露しているのである。
　

表３-１　現代統計学の枢要な概念とその特長 　 １．「母集団　vs. 標本」概念の確立 ―　「母集団　vs. 標本」概念に関する構図 　 　　　　　　 　　抽出(sampling) 母集団　　　 　　　→　　　 　　　標本 (population)　　 　　　　　　　　(sample)　 　　 　　　　　 　　　　← 　　　　　　　　　推定(estimation) 　　　　　　　　　標本で獲得した結論の一般化(標的は母集団) 　　　　　　　　　誤差の発生と精度の制御

　
問題３－３　現代統計学の特長が体感される例として「選挙速報」について考察すること。体験した同様な例があれば、挙げること
　
1）拙著「らくらく生物統計学」、第１章、中山書店
2）拙著「統計学超入門」、第II部第１章、篠原出版新社
　
[topへ]

---

第４回　現代統計学の根幹としての統計学的仮説検定(推定)　（2007/08/21）
　
―　統計学的仮説検定の仕掛けの解明からsignifcantosis(有意差症候群)発症機序の解明と治療法まで
　
　「統計学的仮説検定」という重要な概念にも、有効性ばかりでなくて、限界がある。そして、限界とは何かが十分に理解されていない現実がある。今回は、限界は何か、それに起因する誤解とは何かを指摘して、それらからの脱却への道を示そう。
　
４．１．統計学的仮説検定の手順
　最も典型的である、「２群の平均値の差に関する、対応のないｔ検定」を例に解説する。検定というものの基本的考え方・仕掛けは、全てこのｔ検定と同一の基盤上に成立している。ここでは、ｔ検定の式の誘導は断念して、誘導された式について、その実態を解明しよう。
　

　
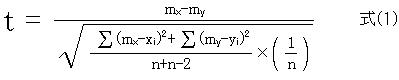
ここで、
ｘ・ｙは、ｘ群とｙ群との２群、
ｘ_iは、ｘ群の個々のdata、ｙ_iは、ｙ群の個々のdata、
ｘ・ｙは、同一のバラツキ(標準偏差ＳＤ・σ)を有し、正規分布する母集団から抽出された標本(sample)、
ｉ＝1，2，．．，ｉ，．．，ｎ、
ｍ_ｘは、ｘ群の平均で、ｍ_ｘ＝（Σｘ_i）/ｎ、ｍ_ｙは、ｙ群の平均で、ｍ_ｙ＝（Σｙ_i）/ｎ、
ｎは各群の例数で、この場合、話しを簡潔にするために、同一例数/群、
とする。
注：Σで拒絶反応が出る読者には、拙著「統計学超入門」、第１章、篠原出版新社を奨める。
　
　さて、この場合の統計学的仮説検定(statistical test of hypothesis)の構成は、
(i)ｘ・ｙ群ともに同一母集団から抽出された標本であると仮定する。
―　つまり、母平均：μ_ｘ＝μ_ｙ、換言すれば、差δ＝μ_ｘ－μ_ｙ＝０、これを帰無仮説(null hypothesis)と呼ぶ。なお、上記σについても、同一(δ_ｘ=δ_ｙ)の仮定
(ii)この条件下で、式（1）で計算／観測されたｔ値が、どの程度の確率／頻度で出現するのかを理論式を用いて計算する。(これがｔ分布の表になる)
(iii)当該頻度が一定水準を越えて「稀」であれば、帰無仮説を棄却(reject)して、対立仮説(alternative hypothesis；差δ＝μ_ｘ－μ_ｙ≠０)を採択(accept)する。一定水準を越えない場合には、棄却しない。「一定水準」を「有意水準α；level of significance　α」と呼ぶ。αは、ご承知の如く、一般には、5％に設定される。
(vi)帰無仮説を棄却できたときに、観測された差は統計学的に有意である(statistically significant)と言う。
　
４．２．統計学的仮説検定の仕掛け
　前述の手順を、機械的に暗記するのではなく、仕掛けとしてbreak-downして掌握することが肝要・急所である。つまり、式（1）の内容・仕掛けを把握し、両群で母集団でも差がない場合の式（1）の挙動はどうなるかを理解することである。
(i)式（1）の分子の理解は簡単である。観測された平均ｍ_ｘ、ｍ_ｙは、類似した値が出現することが期待されるので、０近傍の値になることが期待される。
(ii)分母が曲者である。前の半分が、実は、母集団のＳＤ・σを推定するものである。後の半分がとなっている。かくして、実は、分母全体で以って、標準誤差¹⁾を形成しているのだが、ここでは、これ以上追及しない。
　ここでの急所は、
(iii)帰無仮説を想定しているので、つまり帰無仮説下であるので、分母が０でない限り、式（1）は、０の近傍を揺らぐことになる。
(iv)逆に、稀にではあるが、「偶然」、正規母集団から、ｘ群では大き目のdataを、ｙ群では小さ目のdataを、(その逆も然り)抽出することもある。それは、分子(ひいてはｔ値)の０からの乖離に帰結する。当然ながら、「偶然」による乖離の程度が大となる確率は減少し、その出現頻度は、より「稀」になる。
(v)実は、統計学的仮説検定法とは、こうした「偶然」によって招来される、「見掛け上の差」に対処する方法なのである。つまり、観察された差(正確にはｔ値)が、偶然により発生したと仮定したとき、余りにも確率が小さくなってしまう場合には、偶然(偶発)と考えることを断念(帰無仮説の棄却)して、必然(必発)が存在するとする手法が仮説検定なのである。
　
４．３．対立仮説下でのｔ検定の式の挙動
　統計学的仮説検定の有効性と限界に関して蔓延する誤解を解決する急所となるのが実は、式（1）を対立仮説下で考察することである。しかし、初級教科書では、一般的には言及されていないのが問題だと考える。
　対立仮説下の挙動を考えることの重要性の1つには、現実の研究現場で一般に標的とする２群に差があることを期待しており、差がないことを期待するものではないことである。「同じ新規薬剤の同じ用量を同じ経路で２群に投与した。さあ差があるだろうか？」なんで馬鹿げた研究はしない。
　そうなると、式（1）の対立仮説での考察の方が研究・試験の現場にmatchしているのである。その観点から式（1）の挙動を解明しよう。
(i)対立仮説下の式（1）の挙動解明には、3つの因子があることに注目することである。
(ii)統計学的に有意とするには、「ｐ値＜有意水準α」を得ることであり、これはｔ値が大と連動する。ｔ値大とするには、
(iii)母集団での両群の平均値μの差δが大であること⇒分子大が期待できる。⇒ｔ値大が期待できる。
(iv)母集団でのバラツキσが小であること⇒分母小が期待できる。⇒ｔ値大が期待できる。
(v)最後がdark horse？としての「例数」である。例数が大であること⇒分母小が期待できる⇒ｔ値大が期待できる。
　
４．４．統計学的仮説検定に関して、あなたも犯している？基本的かつ恐るべき誤解！
―　signifcantosis(有意差症候群)：Ｓignificant(統計学的に有意)とＮot Ｓignificant(統計学的に有意でない)との解釈に関する誤解
　上述の解明により、世間で蔓延する以下の各種誤解(有意差症候群)の治療が可能となる。表の形で整理しておこう。
　

表４-１　signifcantosis(有意差症候群)の症状と治療法 その１．「統計学的に有意」であるので、「専門学的に有意」である。 ―　母集団での微小な差δであっても、例数を↑(極端な場合には∞)すれば、必ず、統計学的には有意となる。しかし、だからと言って、当該微小δが、専門学的に(例：臨床学的に)意味があるのか？と考えることがこの病気の治療・治癒への道を開く。 ―　最近経験した例では、25,000例もある場合には、採り上げた因子１０数個全部が統計学的に有意となった。それも、ｐ＜0.0001となった。 ⇒　観測された差の大きさを論じる新たな習慣を身に付けることを奨める。もしくは、「検定」よりも「推定」を奨める。 その２．「統計学的に有意でない・ＮＳ」であるので、「同等」である。 ―　例数を↓、また、母集団のバラツキが操作可能であれば、σ↑、つまり、いい加減な管理など、努力をしない程、同等が主張できる。しかし、それで良いのかと考えることがこの病気の治療・治癒への道を開く。最近では、「非劣性」2)の検証でこうした論法への歯止めが掛けられるようになったので、論文投稿して「非劣性の検証をするように」と突き返されて自覚するのも最終的治療法であろう。 その３．「天下のｐ値が小さい程、統計学的により有意」であるので、「ｐ＜0.01とｐ＜0.001とでは後者での差はより大きい」。 ―　例数・バラツキが比較している２つのcaseで、同一であれば、それは間違いではない。しかし、これらが異なるときには、否である。 ―　観測された差の大きさを論じる新たな習慣を身に付けることを奨める。もしくは、「検定」よりも「推定」を奨める。

　
1）拙著「らくらく生物統計学」、中山書店
2）拙総説「試験における検証法―優越性・非劣性・同等性―と具体的留意点」、月刊PHARMSTAGE、第２巻、第１０号、64-70頁、２００３年
　

　
[topへ]

---

第５回　統計学的仮説検定(推定)の限界　（2007/09/04）
　
―　統計学的仮説検定(推定)法でも対処不能なもの。汝の名はbias！
　
　「統計学的仮説検定(推定)法」(以下、統計学的手法)という有用な手法にも、限界がある。そして、限界とは何かが十分に理解されていない現実がある。今回は、限界は何か、限界に関する誤解とは何かを指摘して、それらからの脱却への道を示そう。解説する理由として、前回の解説でsignificantosisからの治癒・脱却を果たして、その次に征圧・脱却すべきが、統計学的手法の限界を悟ることが極めて重要であり、この悟りを得て初めて、科学的に妥当な情報獲得の道が開けて、統計学的思考体得の免許皆伝になるからである。
　潜在意識の中では、「統計学的手法」は、万能であるとの「隠れ」信奉者が巷に溢れていると言っても過言ではないであろう。言わば、統計学的手法は、東洋の諺では、乱麻を断つことが可能な「快刀」、西洋の諺なら、Gordian knot(Gordius王が作った結び目)を一刀両断できたAlexander大王の剣、という信仰である。しかし、この「快刀」「剣」にも、一刀両断が不可能なものがある。いわば、東洋の我が諺では、「弁慶の泣き所」、西洋での「Achilles heel(アキレス腱)」があるのだ。そのものの名は、「bias(偏り) 」である。しかし、それが大半の者において意識的に顕在化されておらず、それこそが問題なのである(That is the question!)。
　
５．１．bias(偏り)とは何か？
　統計学的手法と言えば分かる者でも、biasに初遭遇という読者も中にはいるであろう。そのために、ここでは、理解を容易にするために、biasの具体的で極端な例の解説から開始しよう。なお、今回解説する内容の詳細は、参考文献^１）を参照されたい。
　参考文献^１）２）には、こうした典型的な例として、「米国大統領選挙予測」での大失敗を示した。つまり、１９３６年という電話が富裕層にしか普及していない昔の時代に『リテラリー・ダイジェスト』誌が実施した、事前調査・予測での大失敗の例である。その内容と顛末を表として提示しよう。
　

表５-１　biasの典型的な例 ―　１９３６年に『リテラリー・ダイジェスト』誌が実施した「米国大統領選挙予測」での大失敗 １．事前調査の方法 (1)対象者 ―『リテラリー・ダイジェスト』誌の読者で、かつ電話機を所有する者 (2)調査の手段 ―　電話による調査 ２．調査の命題 ―　米国国民(有権者)は、２人の大統領候補：ランドン候補・ルーズベルト候補のどちらを選ぶか ３．調査・予測の結論 ―　「ランドン候補＞＞ルーズベルト候補」との圧勝 ４．選挙結果 ―　「ルーズベルト候補＞＞ランドン候補」との圧勝 ５．予測の大失敗の原因 (1)当該雑誌読者は、富裕層 (2)電話機所有者は、富裕層 (3)富裕層は、米国有権者の全体を代表していない、一部の層 (4)米国有権者の大半は、ルーズベルト候補を選択

　
　sampling(標本抽出)の対象とした当該雑誌読者＆電話調査は、米国有権者の大半が誰を選択するかという命題の調査という目的のためには、不適切であり、真相に比較して、ランドン候補に不当に有利、ルーズベルト候補の不当に不利にとなったのである。このように真相を歪めるものをbiasと呼ぶ。
　もう1つだけ、身近に日常的に有り得る極端な例を挙げれば、雑誌に掲載された広告で、「この食品は、○○に効きました！と全国から声が寄せられています！」として、有効例の紹介があるなどである。こうしたとき、万一、無効例を全部除去しての報告であれば、これはもう立派なbiasである。体重などは、量の大小を無視すれば、何もしなくても、概略半分が減少、半分が増加するからである。
　
５．２　bias(偏り)の別称・性質と統計学的手法がbiasに無効な理由
―　あなたも犯している？恐怖の厄病biasへの恐るべき誤解！
　このように、biasとは真相からの乖離(偏り)のことであり、参考文献^１）には、弓矢と的との比喩を用いて解説した。つまり、的の「正中」が「真相」とすると、それから「系統的な」「乖離(的外れ)」が「bias」である。「系統的」の意味するところは、偶然に外れたのではなくて、繰り返して矢を射てもそうであるということである。かくして、biasは系統的誤差(systematic/systemic error; 系統誤差)とも呼ばれる。これに対して、偶然誤差(random error)は、繰り返せば、真相の上下(前後)に揺れる性質のために、相殺されて、真相に接近可能とするものである。
　ここまで来れば、前回解説したことを想起すれば、統計学的手法がbiasに原則的に無力であることが想像可能となろう。つまり、実は、統計学的手法は、その本質を洞察すれば判明するように、偶然誤差対策として考案されたものなのである。このことは、表５．１など前述した例においては、たとえ統計学的有意差があったとしても意味をなさないことは容易に類推できることからも納得できよう。
　

表５-２　bias(偏り)の別称・性質と統計学的手法がbiasに無効な理由 １．bias：系統的誤差(systematic/systemic error; 系統誤差) ２．系統誤差 vs. 偶然誤差(random error) (1)系統誤差の性質 ―　真相(真値)からの乖離。(測定を)繰り返しても消失しない。 (2)偶然誤差(random error) の性質 ―　真相(真値)からの上下(前後)の揺らぎ。(測定を)繰り返せば消失する。 ３．統計学的手法がbiasに無効な理由 ―　統計学的手法は、偶然誤差対策として考案された手法でしかない！

　
５．３　bias(偏り)の夥しき種類と３大分類化の試み
―　我流：人の数程(分)、biasの名称の数
―　so many men, so many minds. 十人十色
―　未体系化・整備化・分類化状態の夥しい種類のbiasは、biasへの対処法の概観的把握には障害になり兼ねない？
　疫学までを展望すると、biasの種類は膨大なものとなる。関心のある読者は、参考文献¹⁾ を参照されたい。そこには、２０種類を越える種類が記載されているが、これでも網羅された訳ではない。また、夥しき種類は、biasの侵入経路を示唆するにはしばしば有効であるが、対策・対処法についての示唆は乏しいと感じている。
　このような状況を反映してであろうが、biasの３大分類化も試みられており、その例を表５－３に示す。なお、１）何故、この3つに分類されるのか、筆者は素朴な疑問を抱いているが、その根拠は何かなどについては、余り解説がなされていない。解説のある数少ないもとしては、参考文献^１）４）を参照されたい。２）表５－３の「confounding (交絡)」については、その名が示す通り、biasの名称が冠されていないことからも、これをbiasに組み込まない解説もある。また、「confounding (交絡)」については、多変量解析に代表される、統計学的手法的に未だ打つ手が存在し得ることも述べておく。
　

表５-３　数多のbias の「３大分類化」３） ―　未体系化・整備化・分類化状態の夥しい種類のbiasは、biasへの対処法の概観的把握には障害になり兼ねない？ (1)selection bias(選択bias) (2)information bias(情報bias) (3)confounding (交絡) 注：(3)confounding (交絡)は、biasとしない解説もある。

　
５．４　biasからの脱却法とは何か？
　その回避・脱却の方法は、既に解説した如く、狭義の統計学的手法ではない。それは、試験・研究のdesignである。そして、これまた、その重要性への理解が世間的には極度に不足している。欠乏としても過言ではない。その証拠に、「試験・研究が既に終了してから、さあ統計解析だ！」という研究者がその大半を占めていると言えば、過言であろうか？
　試験designの概略・急所については、次回以降に解説する。
　
1）日本化薬（株）診断薬室 「目からウロコの医学統計学講座」、第２７回・第２８回
2）ダレル・ハフ原著、高木秀玄訳、「統計でウソをつく法」、（講談社－blue backs、1968）
3）K. J. Rothman and S. Green, ”Modern Epidemiology”, 2nd ed., Lippincott Williams & Wilkins, 1998
4）医薬教育IT活用研究会・疫学　「疫学概論」「Lesson17. バイアスと交絡」より
　

　
[topへ]

---

第６回　統計学的接近法に関する流派　（2007/09/18）
　
― Neyman-Pearson流・Fisher流・Bayes流
―　確率に関する考え方の違いが源流
　
　　我々は、「２打席１安打」の者が「俺は５割打者だ」と言ったとき、信じるであろうか？多分、否である。 では、「１０打席５安打：以下、５／１０と表現」ではどうか？　多少状況は変化する。さらに２５／５０、５０／１００ならどうか？割り算したものは、全て５割であるものの、この順に次第に確信・信用するようになるであろう。 この我々の経験的直観を、統計学的に表現したものが信頼区間/信頼限界(Confidence Interval/ Confidence Limit；以下、ＣＩ)と考えると明快である。 換言すれば、我々は、第3回に登場した世間のオジサンに負けずに、ＣＩへの芽生えを意識下に潜在させているのである。すなわち、統計学的用語で表現すれば、「５割」という点推定(point estimation)だけでは不十分で、区間推定(interval estimation)の必要性を潜在意識に有している。
　ただし、困ったことに、このＣＩの解釈に象徴される如く、統計学的解釈(思想)に流派により違いがあるのだ。それらの代表的流派が、これらNeyman-Pearson流・Fisher流(Fisherian)・Bayes流(Bayesian) なのである。 この議論を表として整理と問題提起をしておく。
　

表６-１　Neyman-Pearson流、Fisher流、Bayes流の違いを理解するための突破口 １．我々の直観とＣＩとの縁(えにし) ―　「２打席１安打：１／２」⇒５／１０⇒２５／５０⇒５０／１００の順に確信度が↑との直観(割り合いは同じ５割であるのだが) ２．これを統計学的に表現したものが「信頼区間ＣＩ」 ３．ＣＩに象徴されるように、流派により解釈の違いがある ―　例：平均値(上記例では５割)の９５％信頼区間について、 Fisher流： 「このＣＩの中に真の平均値が入っている確率・確信度は９５％である！」 Neyman-Pearson流： 「そんな馬鹿げたことを！このＣＩの中に真の平均値が入っているかいないかどちらかでしかない！　それが正解だ！」

　
　大半の統計学の教科書では、検定統計量・確率などの統計学的な数式を用いての計算の仕方を教えているだけで、統計学の底流にある概念(concept)についての解説はなされていない。むしろ、それら概念の解説を避けて通っているようにさえ思える。換言すれば、数学的接近法を解説する書物が正統派であり、こうした流派による哲学的なものの考え方の違いは認識するに値しないとでも言えそうな雰囲気すらある。あるいは、「この数式で示したものが全てであり、それ以上でもそれ以下でもない」というような数学万能主義からすれば、議論する余地など皆無なのかも知れない。しかし、筆者に言わせれば、そうした考えも、真理ではなくて、単なる１つの「哲学」でしかない。つまり、「数学は1つの哲学である。それ以上でも以下でもない。」と言いたい。ここで、筆者流には、「哲学」とは、それ自体を真偽の証明の対象にできるものではない、思想・考え方のこと、または証明の可能性があるが現在では未証明の考え方のことであり、科学的視点での用語で表現すれば、「仮説」のことである。 (余談だが、その意味では、「進化論」は、未だに仮説的要素が多い。我々は新しい「種」の誕生を目撃してはいない！)
　教える者や教科書によっては、Neyman-Pearson流こそが「正統派」であって、それ以外は間違いだという論調のものもあるし、そうした教え方(それこそ流派？)が主流である。始末の悪いことに、何故間違いなのかは恐らく解説がなくて、「子曰く」方式で、「議論の余地なく、そうなんだ！」的な論調の解説であり、筆者流に言えば、これぞまさしく、EBM (Evidence - based Medicine)ならぬ、Bland教授流用語でのABM (Authority-based Medicine)的態度ではなかろうか。ともかく、正統的統計学の専門家は、Neyman-Pearson流なので、議論の際には、以下の解説することを理解して、瑣末なことで「無知」との烙印を押されないようにとの忠告をしておく。
　かくして、こうした解説がほとんどなされていない現状であるが故に、以下の解説もどうしても筆者流になることをここに予告しておこう。当然ながら数少ないものの、それらしき解説のある本、筆者がこの問題を考えるためのhint・示唆を与えてくれた本については、ここで逐次引用しておく。
　不思議なもので、いやそれが人の常なのだろうが、これら流派のどれか１つ(の思考方式)に慣れてしまうと、他の流派の考え方が完全なる誤解と考えるようになるのは筆者とて例外ではない。また、既述したように、これら流派に対して最後の審判(黒白の判定)が科学的に既に下されたとするかどうかは、ここでの解説を理解してから、各自が下せば良いというのが筆者流の立場・態度である。
　
６．１．歴史的時間軸・考え方から観た「Fisher vs. Neyman-Pearson」および「彼ら vs. Bayes」
　Neyman-PearsonとFisherは、同時代人である。ここで登場するPearsonは、有名な「相関係数」の考案者のKarl Pearsonの息子である。親のPearsonとFisherの両者は統計学に底流する考え方・接近法の違いで、生涯互いに相容れぬままであったようであり、この辺りのことを物語りとして仕立てたのが「統計学けんか物語」^１）である。今回解説する考え方での流派についての解説は余りなかった (K. Pearson vs. Fisherの「自由度」なる概念におけるbattleが中心) ように記憶しているが、大変面白い本なので、一読をお薦めする。「自由度(degree of freedom)」なる概念も難解であるし、今回の統計学的接近法に関する概念上の違いも、こうした統計学の巨星達が激論しながらも、なお完全和解に至らなかったのであることからしても、我ら凡人が悟りに至るには難解なのであろう。
　Bayesは、歴史的には、彼らよりも大分以前の人である。また、統計学的な接近法も、Neyman-Pearson vs. Fisherとの対決に至る程にはある意味での類似性がないこともあってだろうが、喧嘩の話しは書かれＴいない1^１）。比喩的に説明すれば、Neyman-Pearson vs. Bayesは、最左翼 vs. 最右翼的位置にあり、Fisherはその中間との見方もできよう。
　
６．２．１．筆者流の悟りの境地へ至る道：その1
―　「数式・数学」を一度捨てよ！
―　「母集団　vs. 標本」の違いを悟れ！
―　「確率」なる概念の定義・あり方を悟れ！
　どうも世間の教科書は数学・数式で全てが説明でき、そしてそれで示されることだけが全てだという、数学万能主義が流布している気がしてならない。確かに、数学には、素晴らしい利点があり、４次元以上については、我々はimageすらできないが、数学(代数)的には察知できるし、相対性理論を展開してblack holeを予言したのも数学の役割りが大きかったと言われている。しかしながら、「信頼区間/信頼限界(confidence interval/ confidence limit)」の関する、Fisher流の解釈であるfiducial limitとNeyman-Pearson流の解釈がまさにそれを象徴しているように、数式は同一であるものの、解釈は全く違うのである。 そして、この違いが両者の終わりなき喧嘩、それこそPearson側にしてみれば親子２代に及ぶ喧嘩へと発展したようである。 　ここでの解説が、これら３者の違いについてその哲学的側面を細大漏らさず語り尽くせるとは思っていないし、解釈に多少の過誤があるかも知れない。しかし、読者にとり、この難問の突破口になるべく斬り込みをしているという確信・自信はある。
　突破口へと至る・入る「狭き門」とは何か？　筆者流手法の種明かしをすれば、実はそれは、あの「母集団 vs. 標本」、そして「確率(probability)」なる概念にどのような意味を持たせるか(定義するか)ということがkey wordsである。両者は底流では連結しているであろうし、完全には独立ではないものの、目的とする突破口を開くには、両方を前面に意識した方がbetterであると考える。

　

表６-２　Neyman-Pearson流、Fisher流、Bayes流の違いを理解するための突破口 ―　その「狭き門」へ至り通過するためのkey words １．「数式・数学」を一度捨てること ２．「母集団 vs. 標本」の弁別・それら概念の違いを悟ること ３．「確率(probability)」という概念にどのような意味を持たせるか・定義するのかを悟ること

　
６．２．２．筆者流の悟りの境地へ至る道：その２
―　「神」になる方法を悟ること
―　「神」と「人・研究者」の違い・弁別を悟ること
　これらの意味を表として整理しておいた。
　

表６-３　「極楽」へ至る悟りを拓くための飛躍を可能にする発想法 １．神(天上界)　vs. 人(研究者：地上界) 神の定義：全知全能・既知・自明 人(研究者)の定義：未知・不明(無知ではない！) ２．神になる方法 ―　想像界(idea＝ιδεα(「イデア」と発音)の世界、Plato＝Πλατωνの観念論) 　に身を置くこと ⇒　神になることが「可能」　 ―　現実界 ⇒　神になることは「不可能」 ３．想像界の素晴らしさや利点 数学的例： ｆ＝1/ｎの式でｎ⇒∞のとき、ｆ⇒０は、誰でも理解可能 しかし、現実界では、ｎの数を特定した瞬間に、それはｆ＝０とはならない。 統計学の世界での象徴的な例： ＳＥ(標準誤差)＝ＳＤ(標準偏差)/√ｎなので、ｎ⇒∞のときＳＥ⇒０

　
６．２．３．筆者流の悟りの境地へ至る道：その３
―　「数学的model」がＵＦＯだと悟ること
　統計学の世界で、神になるために人に与えられた「３種の神器」がある。それが「数学的model」と考える。その典型的な例が「正規分布(確率密度分布）」である。これを例えば、「母集団」として、つまり、頭の中で、ideaとして想定して用いれば、悟りへさらに大きく接近できるのである。第３回での世間のオジサン達の「近頃の若い者は論法」の標的は、「母集団」としていることが素晴らしい発想だとした。 さらに、オジサン達の「母集団」的思考法を、「数学的model」で以って「母集団を数学的modelとして把握すること」へと飛躍させ、完成させるのである。
　

表６-４　「極楽」へ至る悟りを拓くための飛躍を可能にする発想法 １．「数学的model」が「母集団」だと悟ること ２．その豊富なご利益 ―　本文を参照

　
　かくして、母集団における母平均μや母標準偏差σを規定しさえすれば、我々地上界の人・研究者は、そこからｎ例数を無作為抽出する例の構図(第３回)が完成する。 ここまで悟りの境地に到達すれば、後は極楽の入り口が目前である。 いや、もう既に大半の読者が極楽へ到達し、その美しい、大panoramaを満喫しているはずである。 そうである！我々が手にする (標本という名の) dataは、有限個でしかなく、そうである限り、真の平均(母平均)や真の標準偏差(母標準偏差)を「誤差」なしには捕捉できない。 無限個抽出すれば可能であるが、それは、最早神の領域であり、研究者には不可能なことである。つまり、例えば１０例の標本からその平均値を求めても、母平均μ＝１００のところを、ｍ＝９８とか１０２とかになるであろうし、１００になったとしてもそれはマグレ・偶然でしかない。母標準偏差σについても然りである。実は、こうした構図を明確化したものがNeyman-Pearsonであると考えると、眼前の霧が晴れて、流派の違いが浮き彫りにされる。
　
６．２．４．筆者流の悟りの境地へ至る道：その４
―　最後の扉を開く鍵：それは「Neyman-Pearsonは神である」ことを悟ること
　もう１つ最後の鍵を与えて「天上界」への扉を開こう！それは、言わば、Neyman-Pearson流は自分達の身(観点)を「神」として天上界から地上界である「下界」を見下ろす視点なのである。Neyman-Pearson神と比喩した^２）のは至言である。
　想像界・空想界において、人が神になったと想定すれば、研究者を見下ろして、「ああ今度は、あいつらは、真値１００のところを９８としてしまったぜ！　under estimateだね！　愚かな者よ！」という「ご託宣」が可能になる ^３）。
　これが、更に象徴化されるのが「信頼区間」の意味である。Neyman-Pearson神ではどのような解釈をするのか？Fisher(流)ではどうだろうか？ここで、問題として出しても良いが、冒頭の両者の「仮想的対話」にしたことでもあり、解答を言ってしまおう。代表的な例として、平均値の９５％「信頼区間ＣＩ」について、先ず、Fisher(「漁師」なる愉快な比喩^２）もある)は、地上界・下界に身を置いて(これがまさしく「研究者」の立場である！)、今回の研究のdataからＣＩ上限が１２５、下限が７５であったので、真の平均値μは、最大でも１２５、最小でも７５ということ、つまり、この範囲(漁師で言えば「網」)の中にμが入っていることが、９５％の「確率・確度」で言えるとする。 「網：ＣＩ」の中に「魚：μ」を捕捉した「確からしさ」が９５％なのである。これは我々の感覚からは違和感はないであろう。これに対して、Neyman-Pearson(神)は、天上界から、「ああ、今度のdataからのＣＩでは、μが入っていねえや！　間違えちゃったぜ！」などと他人事？として研究者を不憫に思うことになる。つまり、彼らのＣＩに対する解釈は、投げた網ＣＩを特定した瞬間に、魚μは捕捉された/されなかったのいずれかでしかない。
　しかし、人・研究者は、μが分からないから研究するのであり、その点では、Neyman-Pearson神の立場には決して身を置けない宿命である。そして、新規薬物候補の薬効が分かっていれば、「治験」なんぞ、無用の長物(百害あって一利なし！)でしかないのである。
　それでは、Neyman-Pearson(神)は、９５％にどのような意味を持たせるのか？それは、このように何度も何度も繰り返し、網を投げるとき、９５％の「割り合い」で魚を捕捉できるというものであり、それが頻度論者(frequentist)と呼ばれる所以である。ここで、意地悪に、Neyman-Pearson神に天上界から下界に降臨して貰おう。つまり、研究者の立場に身を置いて貰った場合のＣＩの解釈について講釈を受けてみよう。それは、「当該研究でＣＩが特定されたのだから、このＣＩ中のμが入っているかどうか私には分からない！入ってないかも知れん！　言えることは、こうした研究を繰り返したとき、１００回中９５回はμを捕捉できるということだけだ」というものである。「そんなもん、他人事みたいによう言えるな！あなたは繰り返すのか？」と聞きたいものである。これは、最近実施されるようになった「meta-analysis」でも同様であり、複数の研究(いわば一種の繰り返し)を併合して作成したＣＩについても然りである。
　次に、こうした頻度論者の確率の定義と関連して留意すべきことを述べよう。先ずは、頻度論者の立場では、「確率」なる用語は、「割り合い」・頻度として定義されるもの以外にみだりに使用すべきではない。そのために、ＣＩのときにも、９５％「信頼係数」と呼び、９５％「信頼確率」とはしていないことが今や理解できるであろう。
　そしてまた、かつて学校で学んだ「順列・組合せ、確率・統計」において、サイコロなどの例において、「正しいサイコロを振るとき、１の目が出る「確率」は、１／６である」という表現に強い違和感を感じたのは筆者だけであろうか？この表現をすんなり理解できる読者に今回の解説は不要であるが、そうではなかろう。多分、この表現をそのまま素通りしただけのことであろう。そしてこの表現こそが、まさにNeyman-Pearson流を継承したものに他ならないと筆者は思う。「正しいサイコロを振るとき、次に１の目が出る「確率」は、１／６である」という表現の方が人情・直観として、自然でなかろうか？しかし、それでは、次回と特定していることになり、その限りでは、時制的に「未来」であっても、神には先刻既知事項なのである。この点からは、ＴＶで常識化している「明日の降水「確率」」という表現は、違反である。
　
６．３．Ｂａｙｅｓ流の立場
―　未確定のことには「確率」
―　事前確率(prior probability) vs. 事後確率(posterior probability)
―　仏の顔も３度まで：繰り返しとそれによる事後確率の精度向上
　Bayes流の特徴・本質を明快に解説した爽快感溢れる比喩として「源義経がジンギスカン/チンギスハ－ンになった「確率」」という解説がある ^４）。ここまで来た読者には今やその本質が看破できよう。ここでの要点は、歴史的事実は、Neyman-Pearsonに言われるまでもなく、真偽の何れかである。しかし、人には、その真実は不明であり、「可能性」は０ではない。「確率」の定義がそれほどに厳格であるのならば、「可能性」で一向に構わない。そうした不明な過去について研究するのが「歴史学」であろう。「ヤマタイ」国が奈良なのか佐賀のヨシノガリなのか、はたまたそれ以外なのかが確証がない限り、人はそれを議論する価値があり、佐賀で遺跡が発見されたことで、人は「ヨシノガリ」説の確率・可能性↑したと自然に理解する。
　すなわち、時制的観点から論じれば、「未来」は当然として、「現在」、そして「過去」までも、人にとり、未知・不明である限り、「確率」として扱うこと歓迎という立場がBayes流である。
　この立場ならば、サイコロ問題はどうなるであろうか？　解答してしまえば、前回の「目」について不明であるのならば、確率の扱う範疇に入る。例えば、サイコロは既に振られて止まっている状態であるが、ツボの蓋が閉じられたままであるような場合が象徴的な例である。確率は１／６である。現在振って未だ転がっている状態でも、確率は１／６、未だ振らぬ次回についても同様である。
　診断検査した結果により「癌である確率が９５％」という例を挙げよう。投げた「網」の中に「魚」を捕捉している確率と言うのには、現実味を感じなかった読者もこれには真剣に耳を傾けるだろう。当然Neyman-Person流では、あなたは癌であるかないかのどちらかであり、９５％の確率というのは間違いである」となる。確かにそうではある。しかし、「集団検診では、６０％であったものが、精密検査により９５％になったんだ！」という発想は自然であり、聞く側にもそうである。我々もこの点では、Bayes流なのであろう。つまり、神ならぬ人の身である限り、追加情報により確信度↑していく接近法なのである。比喩的には「仏の顔も３度まで」という対応法と通じるものがある。換言すれば、それが、人が神へと至る無限階段を上る道・接近法(∞で神になる)との哲学なのだと解釈できよう。用語として「確率」が駄目ならば、「危険性risk」「可能性」でも構わない。
　こうした接近法のための道具となっている概念が、事前確率vs. 事後確率(posterior probability) であり、追加情報により、事後確率を更新して、確信度↑を図ることになる。また、その確率の性格上の特徴からして、「客観的確率」の対語としてのbelief(信念)との意味合いを込めて主観的確率(subjective probability)とも呼ばれる。しかし、特定の個人の主観という意味ではなくて、神ならぬ人という者が共有できるものだと言えよう。
　余談だが、事前情報の無の場合に対応法の１つとして、均一・一様な確率(例：割り合いの例では、１／２、５分５分)という仮定が一般になされる。「確率」という概念の構築に寄与した者の代表的な１人であるPascalの随想録(Pense'e)には、「神が存在するかしないかは、５分５分である。それであれば、私は存在することに賭ける」という趣旨のことが書かれていたように記憶している。これは、事前確率に通じるものである。
　また、上述のような立場なので、「標本　vs. 母集団」という概念の芽生えはなく、未成熟だと思われる。
　
１）安藤洋美、「統計学けんか物語」、海鳴社、1989年
２）佐久間昭、「薬効評価1―計画と解析」、東京大学出版会、1977年
３）拙著、「らくらく生物統計学」、中山書店、1998年
４) 林周二、「統計学講義」、丸善、1984年
　
[topへ]

---

第７回　統計学的手法としてのparametric法　vs. non-parametric法　（2007/10/02）
― 盲目的にparametric法であるべきなのか？
　
７．１．この問題に対する読者の現状認識をするための診断test 　診断testから開始する方が、自分の現在の認識度・理解度も点検できて、理解が促進されるであろう。
　

＜＜診断test＞＞ １．比較しようとする対応のない２群は、正規分布に従い(つまり、dataが正規分布の母集団から抽出され)、かつ、分散σ2も同一とする。 このときには、parametric検定であるｔ検定が最善であることは当然である。しかし、それと同時に並行してnon-parametric検定であるWilcoxonの順位和検定を実施したとする。つまり、t検定をした、同一dataにWilcoxonの順位和検定をする。前者のｔ検定で１００回samplingして、８０回が統計学的に有意となった場合に、後者では、次の内のどれになると思うか？　解答すること 解答１．８０回／１００回に対して、半分に低下して、　　　４０回／１００回 解答２．８０回／１００回に対して、いやもっと低下して、　２０回／１００回 解答３．８０回／１００回に対して、ほとんど低下しないで、７６回／１００回 ２．たとえ、対数正規分布(dataを対数変換すると正規分布になるもの)したとしても、せっかく連続量dataとして測定し、詳細・豊富な情報を収集したこと、中心極限定理によりｔ検定が機能することから、ｔ検定しないと情報の損失が大きい。 ３．non-parametric法では、ＣＩ(Confidence Interval)算出が一般的に面倒なことが、non-parametric法が使用されない理由である。

　
　若干の寸評をしておこう。
診断test１．
　正解は、解答３である。読者が、これへの正解を得ることで、今回の議論の８０％が解決・解消すると筆者は考える。これを認知した上での「高邁な議論」をしよう！　大半の読者には、それ以上の議論は最早不要化するのではないか？　言わば、嗚呼勘違い！としての「一番多い勘違い」であり、かつて筆者も何十年前には、そう思っていた。それのbreak throughの契機は、後述するConover的な両法の検定の併用を通しての確固たるevidenceの獲得であった。
診断test２．
　特に少数例(概略２０例前後)においては、比喩的には、轟音とともに崩壊することをしばしば体験して来た。(勿論、対数正規分布と判明していれば、対数変換後にｔ検定はＯＫ)
診断test３．
　本音としての大勢的誤解とは直結していないと考える。研究者達の間で、ｐ値崇拝主義者が跋扈する中で、推定としてのＣＩ崇拝者は現在においてすら皆無に近いとの印象を筆者は抱いている。
　
　この話題を解説した教科書は、余りないが、幸いにかなり詳しく総説的に、しかも、私見も交えて解説している珍しい格好の教科書２冊にtimelyにも筆者が最近遭遇した。この話題も「このcolumn」で扱うべきものの１つとしての価値がある、重要なものである。そう考える最大の理由は、世間一般的にかなりの誤解が流布していると筆者は感じていることである。
　
７．２．両者についての解説：parametric法・non-parametric法とは何か？
　先ず、「このcolumn」の読者の中には、parametric法とnon-parametric法との用語について、明るくない方も想定されるので、そこから解説を開始しよう(表７－１)。
　

表７-１　parametric法　vs.　non-parametric法 ―　両者についての解説：parametric法・non-parametric法とは何か？　 　 １．parametric法とは何か？　 ―　parametric検定の代表例である、「対応のないｔ検定」を例にすると、 ⇒　その他も手法も同様であることに注意 1)model(ιδεα：イデア)として、分布(代表的には「正規分布」)を想定・前提・仮定して、分布を規定するparameter(母数)に依拠して、検定・推定法を構築する接近法 ⇒　その当然の帰結として、扱うdataは、体重・身長のような「連続量」が最低限度の前提 (i)正規分布におけるparameterとしては、平均値μと標準偏差σがこれに該当 (⇒　余談：「分母」や「例数」のことを、「母数」という術語の誤用が見られるが、parametricの本当の意味が理解できていないことの自らの暴露する？ので注意！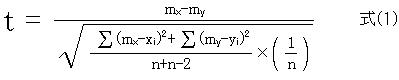) (ii)ｔ検定の構築を観ると、ｔ統計量は、第４回で紹介した通り、 　 　 ―　分子は、２群の標本から得られる各平均ｍとその差とから構成されている。これにより、母集団平均μの推定(つまり、平均というparameterに依拠した推定)を指向 ―　分母も、同様に、２群の標本から得られる分散ＳＤ2に依拠して、分子を構成する平均の差に関する分散の推定(つまり、標準偏差というparameterに依拠した推定)を指向 (iii)こうした理由から、ｔ検定は、parametric検定と呼ばれる。 ⇒　厳密に言えば、ｔ検定では、比較する２群で、標準偏差・分散σ2が同一であることを前提(これが「等分散性の仮定」)。それが成立しない場合には、別の変法としてのparametric検定が開発されている。 　 ２．non-parametric法とは何か？ ―　non-parametric検定の代表例である、「対応のないｔ検定」に該当する「Wilcoxonの順位和検定(Ｕ検定も同様)」を例にすると、 ⇒　その他も手法も同様であることに注意 1)特別に、特定の分布を規定することなく、検定・推定法を構築する接近法 (i)ただし、どんな分布であっても頓着しないものの、分布の形状は、２群で同一であることを暗黙に想定・前提・仮定 ⇒　こうした特徴から、分布によらない手法(distribution-free method)とも呼ばれる。 ―　この条件の中には、「標準偏差・分散σ2が同一であること」を含んでいるものの、そこまでの詳細は、一般的な教科書の解説にもないことが多い。なお、「等分散性の仮定」に関して、parametric法のときほど神経質になる必要はないというのが筆者の直観 (ii)「連続量」の場合であっても、Wilcoxonの順位和検定の例では、それを順位情報に変換して、それに依拠して検定・推定法を構築(Ｗ検定統計量) ⇒　当然ながら、「連続量」でなくて、最初から「順位情報」しか有しないdata(例えば、｢著効｣｢有効｣｢やや有効｣｢無効｣など)については、この方法が主となる。

　
７．２．この問題に対する解説のある絶好の教科書２つの紹介
　読者が、ここまでの基礎知識を共有化できたので、次に先ほど述べた教科書２冊での「parametric法　vs.　non-parametric法」に関する解説を、少し長くなるが、紹介する。
　
７．２．１　Chapter 10, S. A. Glantz, "Primer of Biostatistics" the 6th ed., McGraw-hillでの解説
　先ずは、篠原出版新社で年内出版を予定しており、現在翻訳中である以下の教科書：
Chapter 10, S. A. Glantz, "Primer of Biostatistics" the 6th ed., McGraw-hill,
からである。Glantz教授は、かつて世界的専門誌"Circulation"の統計学的reviewerを務めたと自著の中でも書いている。
*****************************************
★parametric法とnonparametric法の選択法
*****************************************
　原著者は、この節において、正規分布を例にして、
(i)正規分布は、平均値と標準偏差という２つのparameter(母数、パラメータ)により、完全に規定されること
(ii)標本が正規分布母集団から抽出されたとの仮定が成立している場合、parametricな統計学的手法(ｔ検定など)が検出力の一番高い方法となること
(iii)母集団が正規分布していない場合には、parametric法はとても信頼が置けなくなること
―　これは、平均値と標準偏差（つまりはparametric法の鍵になる要素）が、もはやその母集団を完璧には記述できないからであること
―　実際、母集団が正規性からかなり乖離する場合には、平均値と標準偏差を正規分布の視点から解釈することは、甚だしい誤解に導くことがあること
―　その例として、「対数正規分布」では、平均値の周辺に等しく分布しているというよりは、高い方に右側・上側に尾を引いている (右側にskewed。左右対称でない。対数正規分布がその典型的な例) 場合には、平均値と標準偏差に基づいて分布を推定するとき誤解発生の危険性があること
(iv)同じことが、正規分布に基づく統計的検定法に関してもあてはまること
―　近似的にでも正規分布に従っていないと、これらの検定は間違った方向へ結論を誘導する危険性があること
(v)そのような場合には、標本の観測値をそれらの順位(rank)に変換した情報を利用した検定統計量に変換すること
―　それにより、どのような分布をしているかについて何らの仮定も置かずに、しかも観測値についての情報の大半を保持することができること
(vi)これらの検定法は母集団の分布のparameter、つまり母数に基づかないものなので、nonparametric法とか分布非依存（distribution-free）法と呼ばれること*
*：これらの手法は、標本が同じ分布形の母集団から抽出されたという仮定を置く、しかし、その分布形がいかなるものかについては仮定を置かない。
(vii)標本が正規母集団から抽出された場合であっても、nonparametric法は、対応するparametric法に比べて95％の検出力＊を持つこと
＊注：95％の検出力―　こうした記載は、一般的な教科書には提示されていない点であり、評価できる。残念ながら原著には、そのevidenceは記載・明示おらず、原著者に照会したが、この点については、回答がなかった。翻訳本では、解説のための訳注をしておいた。
(viii)従って、nonparametric法の検出力は、対応するparametric検定法の検出力の計算から推定し得ること
(ix)標本が正規母集団から抽出されたのでない場合は、nonparametric法は、parametric法よりも信頼性が高く、かつ、検出力も高いこと
(x)正規性の確認法として、一番簡便な方法は、標本値をplotして眺めてみること
―　分布の±両側の分散が概略同じでその２～３倍した範囲内に標本が収まれば、正規母集団から抽出されたという仮定と整合するであろうこと
―　もしそうなら、parametric法を使ってもおそらく問題ないこと
(xi)逆に、標準偏差が平均値以上であり、当該変数が正値しか取り得ない場合は、これは分布が歪んでいることの徴候(indication)である（当該変数が正規分布するのであれば、負の値も取らなければならないことになるが、実際の値は負にはなり得ない。）こと
(xii)この手順をもっと客観的にできる方法として、観測値を正規確率紙(normal-probability graph paper)にplotすることや、分布が同じ平均値と標準偏差をもつ正規分布に従うとした場合の予想観測値と観測値とがどれほど一致しているかを、χ2検定すること などを解説して、最後に以下のように締め括っている。
―　筆者注：これら手法は、当然goodではあるものの、正規確率紙plot法は、残念ながら、少数例では機能しない。
　残念ながら、これらの手法はどれも、生物医科学研究(biomedical research)でよくある少数例に対しては、いずれにせよ特別に説得力があるわけではなく、接近法をどれにするか（つまり、parametric法かnonparametric法か）は、確実な根拠に基づくというよりも、多くはむしろ主観的判断や好みによらざるを得ない。
　結局のところ、以下のような見解の相違に帰着する。つまり、ある人たちの考えでは、データが正規分布する母集団由来でないとの証拠がないなら、parametric法を使うべきだと考える。何故なら、これらはより検出力が高く、より広く使われているからである。これらの人たちによれば、研究対象の母集団が正規分布しないとの積極的な証拠がある場合にのみnonparametric法を使うべきである。別の人たちは、nonparametric法は、データが正規分布している時でもparametric法の95%の検出力をもち、かつ、データが正規分布しない場合にはより信頼性が高い、という点を指摘する。また、研究者が自分のデータを解析する時には、仮定を最小限に留めるべきであるとの信念もある。従って、parametric法がふさわしいとの積極的な根拠のある場合を除き、nonparametric法を推奨する。現時点では、どちらの立場をとるべきかについてはっきりした答えはない。おそらく、将来もそのような答えは得られないだろう。
　
７．２．２　Chapter 12, M. Bland, "An introduction to Medical statistics" the 3rd ed., Oxford university press
　次に、篠原出版新社からその著書の1つである翻訳本 ¹⁾が出版されているM. Bland教授の以下の教科書：
Chapter 12, M. Bland, "An introduction to Medical statistics" the 3rd ed., Oxford university pressからである(当該教科書からの以下の引用部分は筆者の訳)。Bland教授は、世界的に余りにも有名な雑誌数誌の統計学的reviewerを務めているとのことである。「有名な雑誌」とは、臨床研究家なら誰でも、一生に一度でもよいから自らの論文が受理されたいと思うようなものである。研究家の読者であれば、銘記する価値があろう。
******************************************************
★parametric法か、それともnon-parametric法か?
******************************************************
　様々な統計学的問題のそれぞれに対して、対応する手法は複数のものが考えられる。これは、ちょうど、各種の疾患に対して、治療法が1つではなくて複数あるようなものである。そして、これら治療法の総合的な効果もおそらく類似しているであろうものの、副作用や他の疾患や治療との相性、あるいは患者の体質との適性により違いを生じる。これが適切な治療法だというものは、1つだけでなくしばしば複数あり、その治療法は、むしろ、処方者の、これらの治療効果に関する判断や過去の経験、あるいは単なる思い入れにより決定される。統計解析での多くの問題も、これと類似している。例えば、少数例だけからなる２群の平均値を比較する場合には、ｔ検定、data変換した後でのｔ検定、Mann-Whitney U検定、あるいはそれ以外のどれかを使用できる。これら手法の選択に際しては、正規性の前提が成立しそうであるかどうか、信頼区間を算出することが重要であるかどうか、計算方法が簡単かどうか、などなどに依存する。統計手法を使う場合に、人によっては、正規性の前提について懸念が強く、可能であればいつでもnon-parametric法を用いるべきだと提唱し、他方では、人によっては、正規性の前提を満足しない場合に発生する過誤についてあまりにも不注意な者もいる。
　筆者は、自分達の解析全体を通してnon-parametric法を用いて来たという者にときどき遭遇する。彼らはそのことが、自らの統計学的潔癖性の勲章でもあるかの如く述べる。しかし、そんな類のものではないのである。彼らの実施する有意差検定は、実際にあるべきものよりも検出力が小さいために、結果は「有意でない」ままになってしまう*1こと、そのときに、差の信頼区間を算出する方が情報量が多い*2だろうときにそうしないこと*3を意味するであろう。
　一般的な誤解として、少数例、通常６例未満では、ｔ検定や回帰など正規分布に依拠する手法は使用すべきではなく、順位を用いる手法をそれに変えて使用すべきだというもの*4がある。筆者は、こうした見解を支持する議論を実際には見かけたことはないものの、こうした見解が無意味であることは、この本の表の例(省略)が示している。こうした少数例に対しては、non-parametric法は、５％有意水準で有意とすることができなくなる。こうした少数例に対する解析には、正規性に基づく手法が必要になる。
筆者注＊１：これについてそれがどの程度なのかの詳細な議論を後ほどする。
筆者注＊２：かつて、「more informative」と拙著 ²⁾ の第１１章で解説した。これらを見ずに、勝手かつ独立にである。両者が同一語句を用いて解説していることで、意を強くした次第である。ただし、両者とも、その理由の解説が不十分と思われる。そのことが、Glantz 流表現では、highly honored P(Glantzは大文字のＰを使用) value時代が存続していることの背景にあろう。ＣＩが情報量が多いとの解説は、拙著²⁾ の第１１章や拙著²⁾ の第１０章や共同執筆した「薬局」³⁾ など
　他方で、non-parametric法は、ｔ分布が必要とする仮定が成立していない場合には大変便利であり、これらの使用を回避することも、同様に正しくない。むしろ、この前提と何を知りたいかということとを念頭におきながら、当該問題に対して一番適切な手法を選択すべきである。(中略)
筆者注＊３：ＣＩ算出不能だからＰ法：世間一般には、ｐ値に血眼(将棋の駒に命を賭けた坂田名人)になる一方で、ＣＩには冷淡・無関心・無視であることを考えるとこの説の論拠は乏しいと思われる。
筆者注＊４：この出典については、Bland先生も不明のようだ。とまれ、彼の著書の翻訳したご縁で連絡・議論は可能ではある。
　
　以上について、debate的形式で要約を試みる。
　
７．３．両者についての架空debate的な論点の要約：parametric法・non-parametric法のどちらを選択すべきか？
　
　　　　　　　 　　

表７-２　架空debate的な論点の要約：　parametric検定　vs.　non-parametric検定
過激度		parametric派(Ｐ派)	non-parametric派(NＰ派)
高度	見解	順位dataも含めてparametric法(以下Ｐ法)だ。	当然、順位dataはnon-parametric法(以下ＮＰ法)だ。Ｐ法は、破綻する。
	理由	中心極限定理の原理から正規近似が大概機能する。 そのためにＰ法は検出力が高い。「少数例(６例未満)」で、ＮＰ法など論外だ。	連続量でも、正規分布でなくては、Ｐ法は破綻する。ＮＰ法は分布無関係だし、検出力も正規分布ですら、Ｐ法の(余り言われないが)９５％もあるので、ＮＰ法で良い。
中度	見解	正規分布の前提が成立する限りＰ法だ。 成立しない場合には、「変換」を試み、成功すればＰ法だ。 それでも成立しない場合に、初めて、ＮＰ法だ。 正規確率紙plot 1)や±２×ＳＤ法(拙著 3) の第５章)で点検できる。ＣＩ(Confidence Interval)も容易の算出可能だ。	正規分布成立であれば、Ｐ法で異論なし。 それが確認されない限り、Ｐ法での破綻の懸念への保険としてＮＰ法だ。検出力も正規分布ですら９５％もある。 　 そう簡単に成立/不成立点検できるのか？ 　 それは、ＮＰ法でもなんとか可能だ。

　
　Bland先生の立場は、上記分類で言えば、「中度」Ｐ派となろう。筆者も概略は同意できる。Glantzは、あくまでの一般論に終始しているが、この点の議論に限定して言えば、重要な点を指摘している。１つは、ＮＰ法の検出力が正規分布の場合であっても、９５％という点であり、２つには、医学研究では、少数例の場合が多いという点であると筆者は考える。
　
７．４．筆者が考える議論に追加すべき重要な３つのpoints
　次の「表７-３」に示す、４点である。
　

表７-３　議論で補足すべき情報：　parametric検定　vs.　non-parametric検定 １．「Ｐ法：ＮＳ(Not Significant)　⇔　ＮＰ法：Ｓ(Significant)」となる実感の体験をしているか？ ２．少数例と多数例とで分けて議論をしているか？ ―　特に、正規性の点検法として正規確率紙plotや±２×ＳＤ法が少数例で機能するか？ 　それと連動することとして、 ３．box-whisker plot(box plot)法(拙著 3) の第５章)の活用を視野に入れているか？ ４．一般的に研究者は、ＣＩを欲しているか？

　
　この内の第１番目のものについて、大変に重要(研究の９９％？の場合において、統計学的に有意差を出すことが世間の目的であろうから)なので、さらに解説しよう。
　

表７-４　parametric検定　vs.　non-parametric検定 ―　「Ｐ法：ＮＳ　⇔　ＮＰ法：Ｓ」を体感しているか？ 　　　ＮＳ　　　　　　　ＮＳ　⇒　問題なし 　　　 Ｓ　　　　　　ＮＳ　⇒　ほとんど出現しない！←paradoxと思うかも知れない！ 　　　　　　　　　　　　　　　　　筆者の経験からしては、劇的なものの目撃は「０」 　 　 ＮＳ　　　　　　　Ｓ　⇒　かなり出現する←paradoxと思うかも知れない！ 　　　　Ｓ　　　　　　　　Ｓ　⇒　問題なし 注：以上の知見(findings)は、世間的・庶民的感覚との乖離であろう。

　
　如何であろうか？　　「Ｐ法：ＮＳ　⇔　ＮＰ法：Ｓ」の結末に対しては、かなりの違和感があろう！　この結末に至る原因に読者は強い関心を抱くはずである。筆者の経験では、それは「外れ値」である。これも、どうやら、生物現象でしばしば見られる「対数正規分布」を、「正規分布するはずだ」と固定観念的にbiasを持って観るためのように思われる(拙著 ³⁾ の第５章、拙著 ²⁾ の第１２章など)。かなりの反論があろう！　極論にはなるが、この事実を、専門家も含めてどの程度認識しているのだろうか。「学窓　vs.　研究現場」との対比をするならば、前者が机上の空論的なpit fallへ陥り易いのではないだろうか。いわば、「Neyman-Pearson vs. Fisher」のbattleにも似た土壌があるのかも知れない。
　これを体感する極めて実際的で現場的な解決法があるのだ。それを開示しよう。それは、Conoverなる人物が実際にどのようそうしたかは、原著に戻れないので不明ではあるが、「Conover的な両方の検定法の同時・並行的使い方」（拙著 ^1）の第１２章)なのである。
　かつて、７例で見つけた筆者の実例もこうして手に入れたものである (拙著 ⁵⁾の第１章の「Ｐ法：ＮＳ　⇔　ＮＰ法：Ｓ」の例)。最近の例としては、Ｄｒ．が自分で実施したＰ法でＮＳとなった一方で、こちらでＮＰ法Ｓとなったことを知って、俄然Ｄｒ．が注目して面談を要請された例もある。
　とまれ、この方法は、power９５％を体感できる効果的な方法であること、非正規分布に対してＰ法が破綻することの実感を体得できる方法であることは、筆者の経験から実証されている。読者もこの方法により、誤認？からの脱却されたい。
　
７．５．筆者が考える、最終的な、両者についての架空debate的な論点の要約：parametric法・non-parametric法のどちらを選択すべきか？
　以下が、最もevidence-basedな議論からなるＰ派とＮＰ派とのdebateとなると筆者は考える。筆者は、最もevidence-basedなＮＰ派であることが判明するだろう。

表７-５　架空debate的な論点の要約：　parametric検定　vs.　non-parametric検定 ―　最もevidence-basedなdebate
	parametric派(Ｐ派)	non-parametric派(NＰ派)
見解	正規分布の前提が成立する限りＰ法だ。 　 成立しない場合には、「変換」を試み、成功すればＰ法だ。 正規性が一番確保できる対数変換の底を使えば良い。「－」dataがあれば、適当に全dataが「＋」になるような値を足せば良い。確かに、足す値によりｐ値は微妙に異なるが。 　 　 　 それでも成立しない場合に、初めて、ＮＰ法だ。 正規確率紙plotや±２×ＳＤ法で点検できる。 　 　 　 ＣＩ(Confidence Interval)も容易の算出可能だ。 ６例以下でのＮＰ法の効用を信じるのか？	正規分布成立であれば、Ｐ法で異論なし。それが確認されない限り、Ｐ法での破綻の懸念への保険としてＮＰ法だ。検出力も正規分布ですら９５％もある。 ＮＰ法は、「変換」のelegantでない点を回避できる。例えば、「常用対数」「自然対数」のどちらかを選択するかで、微妙にｐ値が異なる。また、「－」のdataがあれば、対数変換は使えない。 検出/定量限界値なども、どう処理するかにより、ｐ値が変化し、しかもどれが真のｐ値に近いのか分からない。ＮＰ法では、こうした問題自体*が消滅する利点がある。成立/不成立をそう簡単に点検できるか？ 　 しばしば遭遇する少数例でこれらの点検は十分には機能しない。 議論は、少数例と多数例とで分けるべきだ。 多数例(以下の(iii))では、機能することを認める。しかし、(i)だけでなく(ii)でも機能は困難化する。 また、前者は結果の表示の煩雑性が難点 便宜的・直観的に、 (i)超少数例(１桁後半：６例～９例) (ii)少数例(２桁前半：１０例～９９例の内で、２０例前後) (iii)多数例(３桁：１００例以上) また、これら全部に対して、左記の方法をBox-whisker plotで置換することを、我流だが、提案する。Ｐ法破綻の最大の原因は、分布の非対称性起因と思われ、その点検はBox-plotで可能だ。 表示も±２×ＳＤ法に準じて簡潔だ。 それは、ＮＰ法でもなんとか可能だ。 　 ＮＰ法での検定の有意性検出限界に近いので、Ｐ法という手も認める。(出典が不明で誰が言ったのだろうか？) ただし、６例未満で有意となっても統計学を信じるよりも、研究者としての感性を信じるべきでは？
＊：「８０ｐｇ以下」を「０ｐｇ」、「８０ｐｇ」、「８０／２ｐｇ」とするかと言うような問題

　
　６例未満での「研究者の感性云々」は、我流になるが、「個体内再現性(勝手な用語)」などを検討すべきだとの見解である。つまり、初期段階での手技への不慣れ・実験現場の未整備などの根拠ある「偶然」としておこう。これへの懸念を抱くのが最重要だと信じる。
　
1)　J. Peacock & M. Bland原著、拙監訳、「ＥＢＭ実践のための統計学的Ｑ＆Ａ」、篠原出版新社、2003年
2)　拙著、「らくらく生物統計学」、中山書店、1998年
3)　拙著、「統計学超入門」、篠原出版新社、2003年
4)　「薬局」、2004年10月号、第55巻、南山堂、2003年
5)　拙著、「実践統計学入門」、篠原出版新社、2001年
　

　
[topへ]

---

第8回(最終回)　科学的に妥当な研究の計画：試験designの重要性を考える　（2007/10/16）
―　まとめと展望
　
８．１．日常的な問題を科学的に解決するdesignを考えよう！
　今回は、最終回である。連載の回数に関して、内情を言えば、７回までは、筆者から希望した記憶があるが、＋１回としての第８回目は、依頼者側からの提案である。結果的には、前回の第７回としての「統計学的手法としてのparametric法　vs. non-parametric法」は、筆者としては、飛び入りであったものの、読者には一番の目玉「商品」であったであろう。
　しかし、筆者としては、今回の最終回の命題は、当初から、これぞ最後にと用意したものであることを訴えたい。その背景には、換言すれば、統計解析としての、取り分け、「検定法」への過信・盲信が、その考案者・創案者の意図に反して、世間で流布してしまっている傾向があり、それへの警鐘のためである。
　そうしたｐ値崇拝主義が何故問題なのかを科学的な観点から「mes(オランダ語！)」を入れる題材として、本邦のＴＶ的・お茶の間的話題としての「血液型と性格」について一緒に議論・考察しよう。実は、理想的な試験designはどうあるべきかという視点では、「脚気病因説：高木兼寛(栄養素欠乏説) vs.森鴎外(脚気菌説)」¹⁾という極めて重要かつ興味深いと筆者には思われるものがあるが、これについては別の機会に譲ることにした。両者の科学的検証に対する態度とその問題点については、是非、当該書籍を一読され、自らの研究者としての在り方を考察されたい。
　
８．２．血液型と性格
　「血液型は性格を決定付ける」という1つの仮説は、読者は誰でもご存知であろうが、世界的視点からは、本邦独自のものであると言われる。その起源は、一説によると、血液型の発見があった戦前にまで遡る。記憶・情報が余り定かでないが、当時、旧日本陸軍において、血液型と性格とがlinkしておれば、当該戦士の役割り分担を決定するのに有用だと考えられのだと言う (つまり、例えば、几帳面であれば、銃後の補給部隊担当とか）。この辺りの情報は、筆者としては、精査することもなく、記憶を頼りとしているが、京大理学部出身の竹内久美子女史の著述にその紹介があったと思われる。
　最終回の今回は、本邦だけ？の、余りにもpopularな、この仮説の真偽の程を如何に検証するのかを考察することを通して、研究による検証とは何か、どこが急所か、世間でそれにてついてしばしば何故誤解しているのかを一緒に解明して行こう！　寸評しておきたいことがある。それは、この命題に関する検証は、筆者の感想・直観ではあるものの、最大級の難問であろうということである。しかし、同時に、仮説の科学的な検証を考えるときには、最良の題材でもあろう。また、ＴＶ的な世間では、「血液型と性格とに関連があることは、何万例という膨大なdataから統計学的に証明されていることです」と豪語する怪しげな者もいる。こうした「多数例」論法の問題点として、測定の精度を向上させるにのには有効ではあるものの、bias回避には、原則無効であることを、このcolumn連載の読者は先刻看破したことであろう。これまた、「科学」とか「統計学」とか言う、いわば「ご印籠・錦の御旗・虎の威」を借りて納得させようとしか筆者には思えない。換言すれば、「科学」とか「統計学」に対する冒涜である。そして、最後の寸評は、読者が、ここで、この命題への唯一の正解提示を期待しないで欲しいということである。唯一の解答は、権威者や天から与えられるという発想ではなくて、己の頭で捻出するものだという発想の転換をすることが、ｐ値崇拝主義から脱却し、研究者への脱皮を意味すると言えば、過言であろうか？
　

＜＜命題＞＞ (1)「性格」は、「血液型」により決定される。 (2)あるいは、「血液型」により、「性格」は、予測可能である。 (3)血液型：原因⇒性格決定：結果 という「仮説」を如何に検証するか、妥当な検証法とは何か？

　
８．３．この問題を考察し、結論を出すための参考資料
　既に、早々と試験designに関しても、結論を得られた読者もあろうが、それで本当に科学的に妥当なのかも含めての議論が必要になる。別の連載 ²⁾での試験designに関する筆者の解説が参考になると思われるので紹介しよう(表８－１)。しかし、これとて、卑近ではあるものの、難解なこの命題には、快刀乱麻の働きはしない。むしろ、問題点を指摘するのに、有用であろう。
　

表８-１　試験designの分類 1 　専門分野から観た試験の各種分類法 　1.1 　非臨床試験 vs. 臨床試験 　1.2 　治験 vs. 試験 　1.3 　前向き研究 vs. 後向き研究 　1.4 　固定試験 vs. 逐次試験 2 　bias回避から観た試験の各種分類法 　2.1 　対照を置いた試験 vs. 対照を置かない試験 　2.2 　盲検化試験 vs. 非盲検化試験（open 試験） 　2.3 　無作為化試験 vs. 非無作為化試験 　2.4 　並行群試験 vs. 漸増群試験 3 　検証すべき内容から観た分類法 　3.1 　優越性試験 vs. 非劣性試験、同等性試験

　
８．４．この問題に対する斬り口：biasを如何に回避する/できるか？
　読者にとり、最も考えられそうな試験designから検討しよう。それは、次の表のようなアンケート調査であろう。
　
８．４．１　最もありそうな試験design　―　アンケート調査
　このような調査でどのようなことが判明するだろうか？　そしてどんな点に注意すべきだろうか？　これについても表にしておこう。
　

表８-２　試験design　―　アンケート調査 １．対象と抽出方法 ・無作為に十分な数の対象者(被験者)を抽出 ２．質問内容 (1)自分の性格は、次のどれだと思いますか？ 　―　血液型に対応する、世間で言われる４種類に分類した性格 (2)血液型は、Ａ型、Ｂ型、ＡＢ型、Ｏ型、不明のどれですか？ (3)性格は血液型により決定されると思いますか？

　

表８-３　当該アンケート調査での留意点と判明するであろうこと １．留意点 ・回収率(割り合い)はどの程度か？ ２．判明するであろうこと ・自己申告としての、血液型と性格との関連度 ・血液型と性格とが関係すると考えている者と考えていない者との間での自分の性格に関する関連度に違いがあるかないか。 ・血液型を知っている者と知らない者との間での自分の性格に関する関連度に違いがあるかないか。 ３．問題点 ・回答は自己申告/主観的なものであること

　
　回収率としては、概略であるが、９０％程度は望みたい。回答をしなかった者・回収されなかった者に、一定の傾向があれば、それがbiasになるからである。例えば、それらの者が血液型と性格とは無関係だと確信する者であるとか、性格として面倒くさがり屋だとかである。これを、あえて統計学関連用語で表現すれば、「欠測値(missing data)・欠測例の発生」である。欠測値がbiasを誘発しないための条件は、MAR(Missing At Random)などのようなものがある。つまり、欠測が偶発的に発生することであり、換言すれば、回答者のだれもが等しく欠測となる可能性を有していることである。
　ここで、最大の問題としては、これらは、自分の考える性格、つまり主観的な性格という点である。研究の目的が、性格・適性により、例えば、組織での役割り分担・配置を考慮するということであれば、これでは極めて不十分である。つまり、主観的に判定した性格と実際の性格とが一致することの検証をする必要がある。
　この試験は、研究design的視点から論じると、評価者(rater)と被評価者とが同一であるためにbias発生の可能性があることである。薬効評価試験で言えば、「placebo効果」に該当する。そして、こうしたときには、評価者と被評価者とを分離して、かつ両者とも、「血液型」を知らないように操作/介入(intervention)を講じる。これが最もbias潜入が少ないとされる、double blind study designであう。
　逆に、研究の目的が別のもの、つまり表に示したことであれば、この調査だけで達成されることになる。しかし、それは、お茶の間やＴＶで交わされる他愛もない冗句として効用しかないであろう。
　
８．４．２　当該アンケート調査に妥当性を持たせるための補強法
―　第３者による客観的な性格判定以外での当該方法の補強
　しかし、当該命題にdouble blind designが適応可能であろうか？　難儀な点は、本邦に限定すれば、大半の被験者が自分の血液型を知り、かつ、「血液型に対応する」「性格」を知らされていることである。これにより発生する危険性のある「思い込み」などのbiasを回避する手段は、大変実現困難であり、また、複数の方法が考えられるものの、決定打的なものはないように思われる。「表８-１　試験designの分類」も参考にして、読者も一考して頂きたい。気が付くことの１つとして、bias回避として効果的な手段である、「介入」が当該命題では極めて困難なことも判明するであろう。
　

表８-４　当該アンケート調査の妥当性の補強法 ―　第３者による客観的な性格判定以外での当該方法の補強 １．血液型不明者の血液型を検査して判明させること ―　いわば事前情報によるbiasの回避の可能性↑ ―　これら不明者での関連度と既知者での関連度の違いの有無を検討 問題点 ・「不明」との回答は本当か？ 　―　どう対応するか？ ・血液型検査という「介入」が必要 ―ＩＣ(informed Consent)を貰う。 ２．血液型を介入により変化させること ―　血液型変換を受けた者での調査をする。変換後の型を本人が知っていれば、余り効用はない。 問題点 ―　倫理的に不可能！ ３．血液型と性格との関連性に頓着していない外国人を被験者とする 問題点 ―　「日本人」への「外挿」を考えている場合には、「外挿可能性・一般化可能性」の問題 ４．誕生してくる幼児での前向き研究 ―　知らせないままで、成人するまで？追跡 問題点 ―　倫理的な問題。さらには、cost-performanceは最低水準！

　
８．４．３　当該アンケート調査に妥当性を持たせるための補強法
―　第３者による観察研究(observational study)と客観的な性格判定
さて、評価者と被評価者を分離した方法を採用しよう。残念ながら、これでも全問題が解決されることにはならない。
　

表８-５　当該アンケート調査の妥当性の補強法 ―　第３者による観察研究と客観的な性格判定 １．留意点 ・評価者は、被評価者の血液型を知らないこと ・評価者を複数準備 ・客観的判定基準は設定できないか？ ２．判明するであろうこと ・自己申告としての、血液型と性格との関連度 vs. 客観的評価者での関連度の比較 ・評価者間での一致度の度合い ３．問題点 ・評価者間での判定の不一致

　
８．５　まとめと展望
　評価者間の一致度が低いのであれば、それを高める方法を模索することが必要にあり、その１つの解決策として、「客観的評価基準」の導入があろう。しかし、これも簡単にはできないように思われる。さらに、根本的な問題を指摘すれば、そもそも、ヒトの性格は、当該範疇の４つの型に分類可能であるのか？　当該４つで必要かつ十分であるのか？という点である。この辺りの点についての「妥当性」を如何に検証するのかも潜在する問題である。
　最後に、検定方法について述べていないとの叱責を受けそうである。しかし、これらに比較すれば、それは、芥子粒ほどの問題でしかないことが理解されれば、この連載が読者に役立ったことのevidenceである。
　
1)吉村昭、「白い航跡」、講談社、1994年
2)足立堅一、「目からウロコの医学統計学講座」http://www.shindanyaku.net/、日本化薬診断薬.net
　
足立先生のコラムは今回を持ちまして終了いたしました。
ご愛読ありがとうございました。
コラムへのご意見、ご感想がありましたら、こちらまでお願いします。
　
[topへ]